視頻光學法接觸角測量及原理
測量液體在固體表面接觸角一般有二種方法：天平稱量法和光學法。
天平稱量法是一間接測量法，是薄板法表面張力測量儀的副產物。這一方法只適用于幾何形狀規則的固體表面（如圓柱體和長方形薄板），而且測量的也只能是整個接觸周邊表面（periphery of the wetted surface）上的平均接觸角值，不能只限于測量其中的一個面。
光學法是建立在直接觀測液滴在固體表面的接觸界面的測量法，是一種直接測量法。它幾乎不受固體表面幾何形狀和尺寸的限制，適用性廣，測量模式眾多，而且測量多可在與實際應用相同或相似的條件下進行。自從引入了相機和數字圖像處理后，視頻光學法不但大大提高了測量的自動化程度和速度，減少了人為主觀因素的影響，而且使得測量的精度和準確性也獲得大幅度提高。
所有的測量方法都是建立在某一模型的基礎上，視頻光學法也不例外。如上所述，本法是通過直接觀測液體在固體表面形成的液滴的測量法，通過測量液滴的形狀，尤其是其與固體表面相接觸處（界面）的液面（interface meniscus）形狀，來確定液體在固體表面的接觸角（參見圖1）。基于側面（side-view）觀察法的視頻光學法都采用正交觀測法（也即從正側面觀測液滴和液面的形狀），觀測到的只是通過液滴正中軸線的一截面（orthogonal cross section），所以測量方法在一定程度上是默認了液滴和液面的中心軸對稱性（rotational invariance），認為從某一旋轉角截面測量得到的接觸角也同樣地可以代表所有的不同取向（旋轉角）的截面。
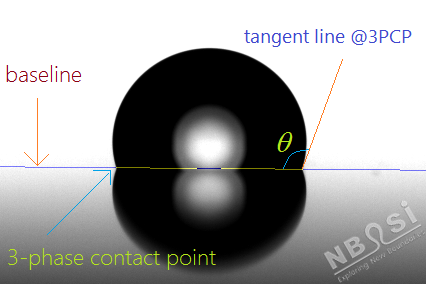圖1：接觸角測量示意圖
除此之外，根據接觸角的定義，它是在液/固/流三相接觸界面處（3-phase contact points, 3PCP），液面與固體表面形成的切線角，是液面走向函數在此位置的一次導數。但實際情況是：恰巧在這一三相接觸界面位置，由于各種因素的影響，液面的輪廓往往不很清晰，這就要求通過測量液面在其它位置的輪廓，并在某一模型的假設基礎上，將其輪廓（走向函數）外推到三相接觸界面位置，以計算出接觸角，θ。這就是為什么接觸角測量時必須采用一定的模型或計算方法的原因。
那么如何衡量/檢測接觸角測量的準確性？
如上所述，測量都是建立在某一模型的基礎上，測量的準確性首先取決于采用的假設模型在多大程度上與實際被測量體系相符合的程度：符合得越好，測量的準確性也就越高。反之，即使測量的重復性再好（有些廠家甚至給出±0.01度），其數值的準確性（與真實數值的偏差）也不可能得到保證。試想一下：一種方法的誤差高達10度以上，而它的測量重復性高達±0.01度，但這沒有意義。
上面我們提到了視頻光學法測量接觸角的一個默認的前提（中心軸對稱性）和必要的模型假設（液滴或液面輪廓走向函數）。采用的液滴或液面輪廓走向函數的模型與真實情況的相符合性在很大程度上直接決定了最終測量得到的接觸角的準確性。
當前運用于視頻光學法測量接觸角的整體液滴或液面輪廓模型基本上有以下幾種：
球或圓（截面）模型：如寬高法，圓法，θ/2-法等
橢球或橢圓（截面）模型：如橢圓法
Laplace-Young模型：Laplace-Young法
其中球或圓（截面）模型是假設表面張力的作用與液滴本身的重力相比，大大超過后者，所以后者的作用力可以忽略。這其實只對體積很小（小于2μl）的水滴，而且當接觸角比較小時，才大致符合。對體積較大，角度較大，或非水液體，此模型的偏差相當明顯，且隨著體積增大，液體的密度增大，液體的表面張力減少，接觸角值增大，這一偏差也將越來越大。當接觸角大于120度、采用的水滴的體積在5μl以上時，偏差可超過10度以上。另外理論計算可以證明，如果采用以球或圓（截面）模型為基礎的計算方法，測量得到的接觸角的數值始終不可能高過約155度，不管液滴的真實接觸角值其實已經遠遠超過這一數值。
橢球或橢圓（截面）模型是在部分考慮了液滴本身重力的影響下，液滴或液面輪廓被壓扁，近似橢圓狀。所以這一方法較圓法更接近真實狀況，得到的接觸角的值也較接近其真實值。但真的來說，當接觸角的值超過90度后，其與真實狀況的偏差也明顯地顯示出來。
當一液滴躺在一平整的固體表面上而處于力平衡（hydrostatic equilibrium）時，它的形狀是由液體的表面張力、液體的體積和液體與固體表面間形成的接觸角而決定的。早在100多年前Laplace和Young就先后建立了描寫這一力平衡的狀態方程（可以參見俯視法中的敘述：光學俯視法測量接觸角以及原理），只是這一方程沒有解析解。一直到最近20年，隨著計算機的發展和應用，這一描寫液滴輪廓的方程才得以部分求解。部分求解這一方程的前提是：液滴和液面呈現中心軸對稱性。
因此對于所有符合這一前提的液滴，無論其體積、密度和接觸角多大，只要其形狀呈現中心軸對稱性，其輪廓就可以用Laplace-Young方程得以準確描述，而且能得到求解，由此就可準確計算出其在固體表面的接觸角（參見圖2）。接觸角的值與液滴的體積無關。
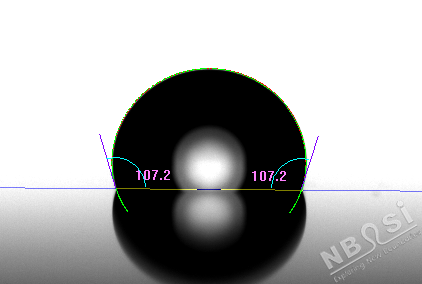圖2：Laplace-Young方法計算接觸角值結果
（圖中的綠色曲線為根據Laplace-Young方程計算得到的最佳擬合理論曲線）
在實際測量中，有些固體表面并不完美，呈現化學（如組成、結構等）或/和物理上（如形貌，取向，應力等）的不均勻性，這一不均勻性會導致液滴和液面不再完美地呈現中心軸對稱性。在這種情況下，雖然Laplace-Young方程仍可準確地描述其形狀，但卻無法求解。此時若仍然堅持中心軸對稱性的假設前提，得到的答案會多多少少偏離真實的液滴形狀，影響其最后得到的接觸角值的準確性。為了更好地對付這種情況下的接觸角測量的準確性，我們的軟件引入了真實液滴法（TrueDrop method），它能近似地，但在多數情況下，相當準確地描述液滴的輪廓走向，而且對幾乎所有的液滴形狀，都能得到相當滿意的結果（當然在中心軸對稱性前提得以滿足時，Laplace-Young法得到的結果永遠是最可靠的）。
總之，要想準確測量接觸角，首先要選擇最接近真實液滴的模型或狀態方程，在這里我們提供了當前商用儀器中最完整的多種模型選擇，再加上我們引入的獨特的真實液滴計算法。其次，選擇的計算方法（模型）符合真實液滴形狀的程度究竟有多好，可以通過觀察實際測量得到的液滴輪廓線與模型擬合線之間的偏差就能很好地判斷。
對于比較完美的固體表面（如許多工業制品的表面），形成的液滴基本符合中心軸對稱性這一前提，此時若采用Laplace-Young法，其準確性可以達到0.1 – 0.5度（注意我們這里說的是準確性accuracy, 而非重復性或精度precision）。對于不很完美的表面，若采用適當的模型（如真實液滴法），接觸角的準確性一般在0.5 - 1度左右。如果考慮到真實固體表面的不均勻性，這一準確性其實已經很高，完全可以滿足各種不同的應用的要求。
影響接觸角測量準確性的另一個關鍵因素是液滴與固體表面相接觸處的基線（baseline）位置的測量（這可以從上面給出的有關接觸角的定義得出）。基線位置對接觸角值測量結果的影響隨著接觸角值的變大而迅速地增加：接觸角越大，由于基線位置測定不準確而導致的接觸角測量結果的誤差也越大。如果測量軟件沒有自動、準確確定液滴基線位置的功能，基線位置只能通過肉眼觀察來確定，那么其實這樣的方法根本不可能達到0.1度的測量準確性，不管采用何種計算方法。而且當接觸角值在90度以上時，由于基線位置誤差而引起的接觸角測量誤差可以高達1-5度左右。
除了通常采用的基于側面（side-view）觀察法的視頻光學法以外，另一種測量接觸角的光學方法是采用從液滴的正上方俯視（top-view）觀察液滴的形狀。
© 寧波新邊界科學儀器有限公司版權所有，未經許可，禁止轉載。